Simultaneous Preference and Metric Learning from Paired Comparisons.

Presented as a Spotlight Presentation at NeurIPS 2020 [bibtex]

The ideal point model for human preference posits that a user's preference for an item (e.g., shoes, TV shows, etc.) can be represented as a point in some space with a set of items. The closer an item is to the user's preference point, called the user's ideal point, the more preferred that item is. The distance under which this "close-ness" is measured is key to understanding how the user makes their preference judgements.

The most common choice for distance metric under this model is the Euclidean distance, which considers each item feature idependently, and assigns each feature equal weight in the preference judgment. These facts are overly restrictive, as humans often consider combinations of features, and prioritize said combinations differently. One way to model this is with a Mahalanobis metric, which parametrizes the Euclidean metric with a symmetric positive semidefinite matrix.

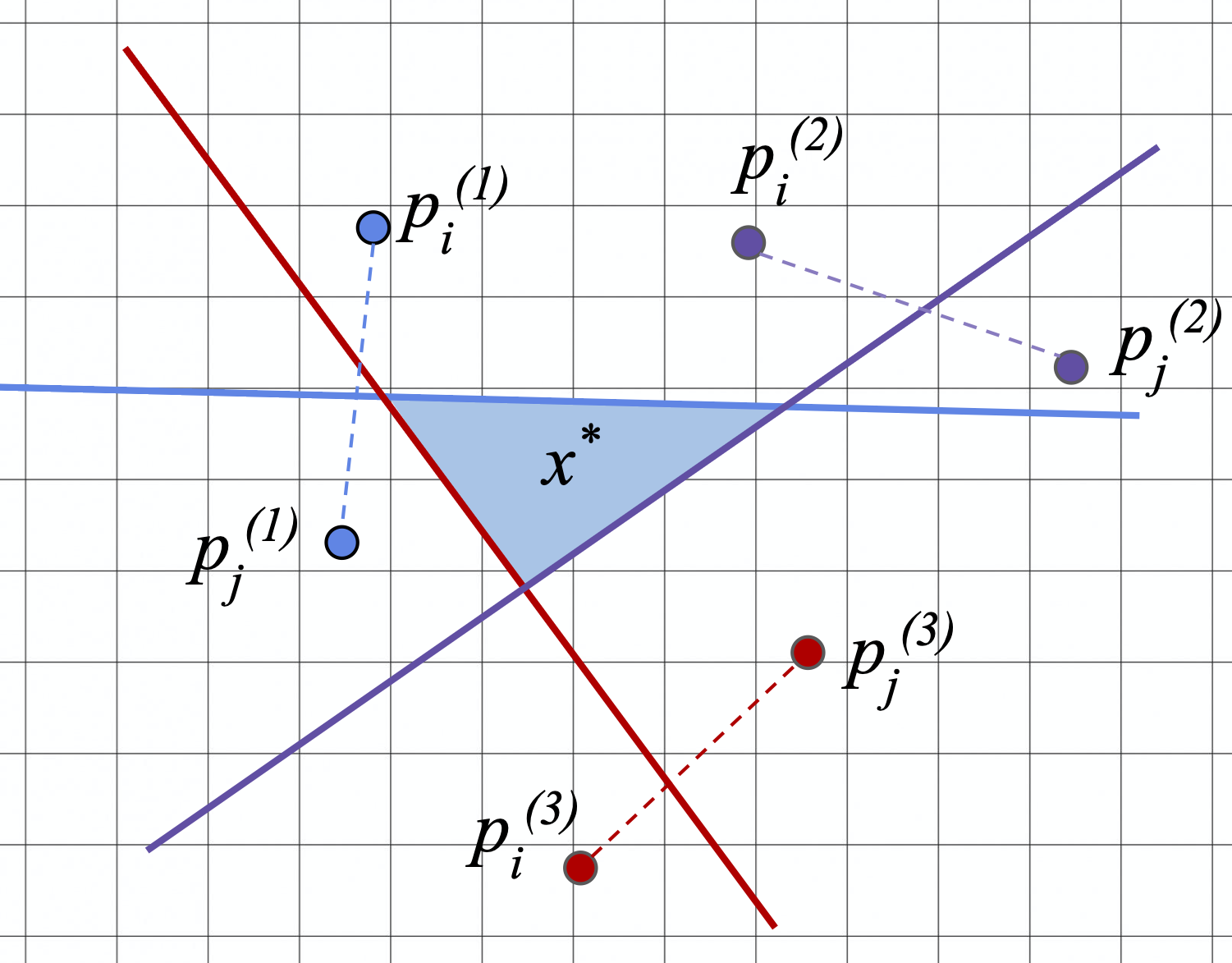
We pose the following question: Using paired comparison queries of the form "do you prefer item A or B?", can we estimate both the user's ideal point and the metric? Each paired comparison response reveals which item is closer to the ideal point, which translates to a halfspace where the ideal point lies. Given enough halfspaces, we can localize the ideal point, as shown above. We propose a simple two-step estimation procedure where we first estimate the metric via semidefinite program, then, with this estimate for the metric in hand, learn the ideal point.

Check out our paper, or the Spotlight Presentation below for more details.